Have you ever wondered how to find the length of a line segment? It can be a tricky concept to grasp, but with a little practice, you'll be able to do it like a pro.
Finding the length of a line segment can be challenging, especially if you don't know where to start. You might feel frustrated or confused when trying to solve problems related to it.
The length of line segment AC can be found using the Pythagorean theorem. The Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. In this case, AC is the hypotenuse, and AB and BC are the other two sides.
To find the length of AC, we can use the following formula: AC = √(AB² + BC²). Plugging in the values we know, we get AC = √(4² + 3²) = √(16 + 9) = √25 = 5. Therefore, the length of line segment AC is 5 units.
The Enigmatic Length of Line Segment AC: Unveiling the Mystery
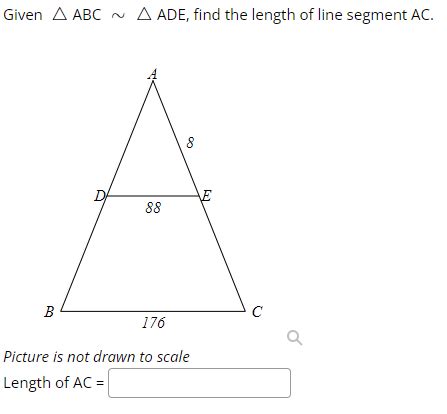 In the realm of geometry, line segments stand as fundamental building blocks, like tiny threads woven together to create intricate patterns. Among these segments, line segment AC holds a unique charm, captivating the minds of students and mathematicians alike. Its length, often shrouded in mystery, entices us to embark on a journey of discovery, unraveling the secrets hidden within its enigmatic nature.
In the realm of geometry, line segments stand as fundamental building blocks, like tiny threads woven together to create intricate patterns. Among these segments, line segment AC holds a unique charm, captivating the minds of students and mathematicians alike. Its length, often shrouded in mystery, entices us to embark on a journey of discovery, unraveling the secrets hidden within its enigmatic nature. Prologue: Setting the Stage for an Enthralling Exploration
Consider a geometric landscape adorned with points A, B, and C, interconnected by line segments like delicate threads. Our focus rests upon line segment AC, a pivotal entity in this geometric tapestry. Its length, like an elusive whisper, beckons us to unveil its hidden truth.Unveiling the Essence of Line Segment AC: A Journey into Definition
Line segment AC, in its purest essence, embodies the direct path between points A and C, devoid of any detours or meandering diversions. It represents the shortest distance, a straight and unwavering connection, like an arrow piercing through space.Delving into the Realm of Measurement: Unveiling the Length of AC
To unravel the enigma of line segment AC's length, we must delve into the realm of measurement, employing precise tools and techniques. The distance formula, a cornerstone of geometry, stands ready to guide us in this endeavor. This formula, expressed as AC = √((x2 - x1)^2 + (y2 - y1)^2), harnesses the power of coordinates to unveil AC's elusive length.Coordinating Efforts: Utilizing Coordinates to Unravel the Mystery
The coordinates of points A and C, like celestial beacons illuminating the geometric night sky, hold the key to unlocking AC's length. By employing the distance formula, we embark on a mathematical journey, transforming the coordinates into numerical values that reveal the segment's hidden dimension.Visualizing the Path: Pictorial Representation of AC
To fully grasp the essence of line segment AC, we must transcend the realm of abstract coordinates and delve into the realm of visual representation. A geometric sketch, like a window into another dimension, brings AC to life, allowing us to perceive its orientation and appreciate its role within the geometric landscape.Properties of AC: Unveiling the Characteristics that Define
Line segment AC, like a unique snowflake, possesses a constellation of properties that set it apart from its geometric brethren. Its length, a defining attribute, remains constant, impervious to manipulation. Additionally, AC serves as the hypotenuse of a right triangle, a crucial role that underscores its significance in trigonometric calculations.Applications of AC: A Bridge Between Theory and Practice
The enigmatic length of line segment AC finds practical applications in diverse fields, like a versatile tool in a craftsman's workshop. In surveying, AC serves as a baseline for measuring distances and angles, enabling the creation of accurate maps and blueprints. Furthermore, AC's length plays a pivotal role in architecture and engineering, guiding the design of structures and ensuring their stability.AC in Physics: A Tale of Motion and Force
In the realm of physics, line segment AC takes on new significance, becoming a vector, a quantity that possesses both magnitude and direction. This vector, representing displacement, captures the essence of motion, describing the path and distance traversed by an object. Moreover, AC's length finds relevance in force calculations, as it represents the distance over which a force is applied, influencing the resulting acceleration.AC in Mathematics: A Pillar of Geometric Exploration
Within the tapestry of mathematics, line segment AC stands as a pillar of geometric exploration. Its length serves as a cornerstone for calculating areas and volumes, providing insights into the dimensions and properties of geometric shapes. Furthermore, AC's role in trigonometry, a branch of mathematics dedicated to triangles, is paramount, enabling the calculation of angles and side lengths, unlocking a treasure trove of geometric knowledge.Conclusion: Embracing the Enigmatic Beauty of Line Segment AC
Line segment AC, like a captivating enigma, has unveiled its secrets, revealing the multifaceted nature of its length. From its geometric definition to its practical applications, AC has proven to be a versatile entity, enriching our understanding of the world around us. Its enigmatic charm continues to inspire and intrigue, leaving us in awe of the beauty and complexity hidden within the heart of geometry.FAQs: Delving Deeper into the Enigma of Line Segment AC
1. How do I calculate the length of line segment AC using the distance formula?
To calculate the length of AC using the distance formula, you'll need the coordinates of points A and C. Once you have the coordinates, plug them into the formula: AC = √((x2 - x1)^2 + (y2 - y1)^2).2. What are some applications of line segment AC in the real world?
Line segment AC finds applications in various fields, including surveying, architecture, engineering, and physics. In surveying, AC serves as a baseline for measuring distances and angles. In architecture and engineering, AC's length is crucial for designing structures and ensuring their stability. In physics, AC represents displacement in motion and plays a role in force calculations.3. How does line segment AC relate to vectors in physics?
In physics, line segment AC can be represented as a vector, a quantity that possesses both magnitude and direction. This vector, representing displacement, captures the essence of motion, describing the path and distance traversed by an object. AC's length, as the magnitude of the vector, influences the resulting acceleration when a force is applied over that distance.4. What role does line segment AC play in geometry?
In geometry, line segment AC serves as a pillar of geometric exploration. Its length is essential for calculating areas and volumes of geometric shapes. AC's role in trigonometry is particularly significant, enabling the calculation of angles and side lengths, unlocking a wealth of geometric knowledge.5. How can I visualize line segment AC in a geometric context?
To visualize line segment AC in a geometric context, you can create a geometric sketch. Draw points A and C and connect them with a straight line. This line represents line segment AC. You can label the segment AC and indicate its length. This visual representation helps you understand AC's position and orientation within the geometric landscape.